Un mostro probabilistico | Il gioco della scienza

Riguardo al problema delle perle delle collane concentriche, che erano rimaste in sospeso, questo è il commento di Manuel Amorós:

“Penso che solo i numeri dispari possano essere una soluzione. Per vederlo possiamo prendere i numeri naturali invece dei colori. La condizione necessaria è che ogni numero sia separato dal suo omonimo da una quantità, e queste quantità devono essere diverse. Dovremmo quindi avere un’espressione del tipo:

1 + 0 = 1

2 + un = b

…

n + t = p

Non può apparire nella seconda colonna Ncon cui e tenendo conto che la seconda colonna percorre 0,1… n-1 e la terza percorre 1, 2… Npossiamo sommare ottenendo (n+1, 2) + (n, 2) congruente (n+1, 2) (modulo n). Allora la condizione necessaria è che (n, 2) sia multiplo di n. Ciò può accadere solo se N è strano.

D’altro canto è una condizione sufficiente. Possiamo collocare i numeri omonimi ad una unità meno di distanza da detto numero. Ad esempio, per N =5:

1 + 0 = 1

2 + 1 = 3

3 + 2 = 5

4 + 3 = 2

5 + 4 = 4″.

Ma il problema ha suscitato altre riflessioni interessanti (cfr commento a Il succo della minoranza), e si presta ad ulteriori approfondimenti.

Il simbionte di Schrödinger

D’altro canto, un commento di Salva Fuster fa sorgere il “meta-problema” del simbionte:

“Il problema dei simbionti mi suona familiare, essendo stato affrontato molto tempo fa. Se ricordo bene, una delle questioni sollevate riguardava la conservazione della massa. Le suddivisioni potrebbero non essere possibili se la capacità di divisione della materia avesse un limite inferiore”.

Anche a me suona familiare, ma poiché la questione del mostro stocastico non è nel titolo, non riesco a localizzarla (qualcuno potrebbe sorprendersi che non controlli tutte le puntate di The Science Game, ma questa è la numero 495). Senza dubbio un lettore diligente troverà l’articolo in questione e potremo tornare sull’argomento. O, meglio ancora, possiamo consultare il Introduzione alla teoria della probabilitàdi William Feller, come suggerisce Francisco Montesinos:

“Per sapere se il processo termina in una popolazione N = 0 o si sviluppa senza limiti, dobbiamo piuttosto vedere se E (numero atteso di discendenti diretti) è <= 1, nel qual caso finisce per morire, oppure E > 1 in nel qual caso si sviluppa senza limiti. Nel caso specifico, poiché E > 1 non morirà mai. Vedi Feller, p. 301 e segg.

Questa opinione contrasta con quella di altri lettori, i quali credono che il simbionte morirà sicuramente. Cosa ci resta? Sarà il mostro di Schrödinger, vivo e morto allo stesso tempo finché non apriremo il caveau in cui è rinchiuso?

Reti paradossali

Per quanto riguarda il Paradosso di BraessCommenti di Fuster:

“Un altro caso del paradosso di Braess potrebbe verificarsi nelle reti a commutazione di pacchetto, in cui l’abilitazione di nuovi percorsi tra i nodi della rete potrebbe causare tempi di invio dei messaggi più lunghi, anche se penso che sia un caso molto simile a quello delle strade.” Al che un altro lettore aggiunge: “In effetti, in generale il paradosso si osserva nel flusso nelle reti. Nel 1990 la British Telecom subì una vera catastrofe nel comportamento della rete.

E ancora una volta i miei gentili lettori hanno riempito la sezione. Devo solo sollevare un problema relativo ad uno degli argomenti discussi recentemente. Come il seguente, proposto all’epoca da Josep María Albaigès nella sua ottima rivista Carrollia:

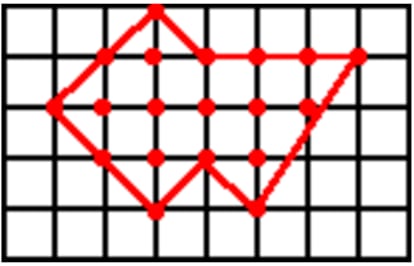
Supponiamo una superficie di piastrelle quadrate di un metro di lato, su di essa disegniamo un poligono fantasioso quanto vogliamo (vedi figura) formato da linee rette che uniscono esclusivamente i vertici delle piastrelle. chiameremo N al numero di vertici che si trovano sulla linea perimetrale e B al numero di vertici all’interno del poligono. Si tratta di trovare una formula che, a seconda N sì Bfornire il valore dell’area del poligono.