La regolarità della 500 e del 2025 | Il gioco della scienza

Dividere un Camembert discoidale in otto parti uguali con tre tagli dritti è semplice… se si tiene conto della terza dimensione, cioè l’altezza del formaggio. La difficoltà (psicologica più che geometrica) di questo problema sta nel fatto che si tende a pensare solo a tagli verticali, e in questo caso la soluzione è tagliare il formaggio a pezzi utilizzando due tagli verticali diametrali e perpendicolari tra loro, più un terzo taglio orizzontale equidistante tra loro le basi.

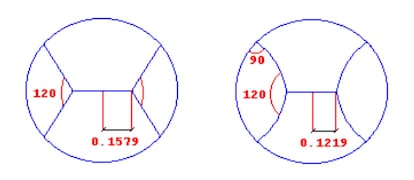
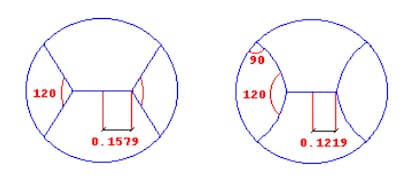
L’altro problema domestico della scorsa settimana non è così semplice. Chiamando n il numero di porzioni, per n = 2 en = 3 le soluzioni sono banali: nel primo caso faremo un taglio diametrale, nel secondo divideremo il formaggio in tre settori di 120º. Riproduco di seguito la soluzione data a suo tempo dall’autore del problema, Josep Maria Albaigès, per n = 4, compresa l’illustrazione originale, tratta dalla rivista Carrollia:

“Per n = 4 le cose cominciano a complicarsi. Ebbene, un taglio secondo quattro settori di 90 gradi darebbe una lunghezza di taglio L = 4, mentre nel sistema indicato nella figura a sinistra è sufficiente L = 3,9624. Questa divisione è stata ottenuta ricordando la nota proprietà che il punto situato all’interno di un triangolo la cui somma delle distanze dai tre vertici è minima è quello che vede questi sotto angoli di 120 gradi. Si può però ancora migliorare: intuitivamente si comprende che, poiché i segmenti rettilinei incidenti sulla circonferenza non sono ad essa perpendicolari, potrebbero essere sostituiti da archi di circonferenza che soddisfacessero questa condizione. Si migliora ancora un po’, arrivando alla figura a destra dove L = 3.9412″.

numeri regolari

Oltre ad essere la prima del 2025, questa è la consegna n. 500 di Il gioco della scienzae sebbene i numeri tondi non siano da sopravvalutare, uno tondo come questo, che in numeri romani meritava una lettera a parte, non può passare inosservato.

Oltre alla doppia rotondità (poiché termina con due zeri), la particolarità matematica più notevole di 500 è che è un numero regolare. I numeri regolari sono quelli tra i cui fattori primi non ce n’è nessuno maggiore di 5 (cioè solo 2, 3 e 5), ed erano di grande importanza presso i Babilonesi (indovinate – o meglio deducete – perché?); I primi venti sono:

1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 25, 27, 30, 32, 36…

1 è incluso perché secondo un’altra definizione (la prima, in realtà), un numero regolare è quello che divide una potenza di 60 (e quindi 30).

Al di fuori del regno della matematica, 500 dà il nome a un gioco di carte con aste e coppie simile al bridge (in cui i giocatori dichiarano in anticipo il numero di prese che si aspettano di vincere). In una delle varianti bisogna ottenere esattamente 500 punti, da qui il nome del gioco.

A proposito, anche il 2025 è un numero regolare, nonché un quadrato perfetto (452). E poiché sia ​​500 che l’anno che abbiamo inserito sono divisibili per 5, rendiamo divisibile anche un quadrato per 5. È molto facile dividere un quadrato in 4 quadrati uguali, ma non altrettanto facile in 5, sebbene ciò possa essere ottenuto attraverso una costruzione geometrica relativamente semplice. Riesci a dividere un quadrato in 5 quadrati uguali senza l’aiuto di un righello? E se si ricorre agli origami, non è nemmeno necessario che siano graduati.

E, infine, non può mancare un piccolo problema legato al nuovo anno:

Per Natale mi hanno regalato due agende giornaliere per il 2025, e visto che me ne serve solo una, conservo l’altra per il prossimo anno che inizia di mercoledì (e non è un anno bisestile). Quanto tempo devo rilasciarlo?

Un nuovo anno e 500 consegne di Il gioco della scienza: doppio motivo per ringraziare i miei lettori abituali per la loro regolarità e commenti penetranti, che rendono questa rubrica più di una semplice sezione sugli hobby matematici.